TWO WAY ANOVA (WITH/WITHOUT INTERACTION) SAS

 Two way ANOVA:  Here, null hypothesis says that the sample means are not significantly different, the difference in their means occurs due to unexplained variability or simply by random chance. Now, in two way ANOVA there are two predictors (categorical) and one response (continuous) variable.

  • Two way ANOVA models are built either by interaction effect of predictors or by individualistic effect of predictors on response variable. 
  • The most significant parameter is F ratio, it test the significance of model and considered as significance ratio of two variances.
  • The higher the value of F ratio the more the significant the model is which inadvertently states there is significant difference between sample means (at least one sample mean differs from other sample means).
  • Remember, it is parametric test, when we don't know the sample distribution or distribution of population from which sample is collected, it's better to test hypothesis using non-parametric test (chi-squared test or  Kruskal-Wallis test for small sample sizes).

Here in this following blog, we are just going through codes and interpretation of results.

System: SAS On Demand Academics


Code explanation:

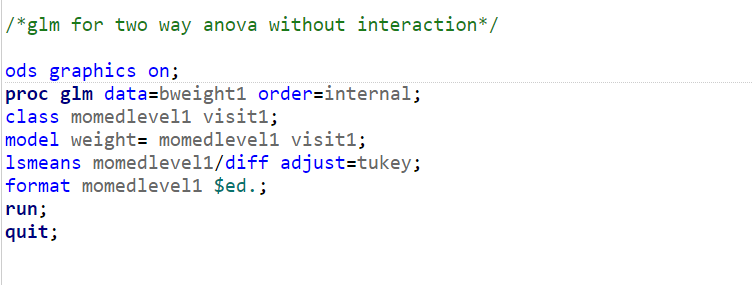
  1. Proc glm : GLM stands for generalized linear models. This procedure is used for unbalanced and balanced data where regression procedure is used for balanced data only.
  2.  Order option: "internal" : the levels present in predictor or class variables are considered the way they are stored in data.
  3. Class: mention categorical predictor variables in this statement.
  4. Model: "Response = Predictor-1 Predictor-2..... Predictor-n" statement;
  5. LSmeans: Least square means, a method to calculate estimated means; here they are calculating means of response variable with respect to level present in one of the class variable (predictor).
  6. Diff/ Adjust: Diff is for diffogram and adjust (multiple comparison test in pairwise combinations: here we used Tukey's test to compare means of all possible pairwise combinations and controls experimental error rate at 0.05 (by default)).
  7. Format: A format is applied on one of the predictor variable.
Data manipulation step prior ANOVA


Code explanation:

  1. The data that was used consist of categorical variables stored in character format.
  2. Put statement: converts numeric data to character.
  3. Keep statement: kept the mentioned variables in output dataset (bweight1).

Result:

First part

First part: 

  1. Two predictors, both of these factors has 4 levels (mom education level and visits to hospital).
  2. 50000 observations were read during generalized linear model procedure.


Second part

Second part:

  1. The first table consist of source of variance, sum of squares, mean square, F value and p-value.
  2. The F value is 150.25 which is quite high (significant model) indicating there is significant mean difference in infant birth weight when compared with four levels of each predictor variable.
  3. Then there is R-squared and various other parameters computed of this model.
  4. Next table, tells the significance or I must say F value of each predictor variables. In one table type one sum of squares computed and in next table type three sum of squares is calculated.
  5. Both of the predictors have significant effect on variation seen in response variable.
check type one, two and three sum of squares:

https://towardsdatascience.com/anovas-three-types-of-estimating-sums-of-squares-don-t-make-the-wrong-choice-91107c77a27a

Third part

Third part:

  1. As you can recall, we asked for least square means in above code for one of the predictor.
  2. LS means procedure tells that is there any significant difference in mean of response variable when we consider different levels of our class/ categorical variable.
  3. The first table tells the computed least square means for response variable against each level found in momedlevel1 (mom education level) variable.
  4. Next, we asked for multiple comparison test: Tukey test which performed significant difference analysis on each of the pairwise combinations of predictor variable. In the 4 by 4 table, we can observe there is significant mean difference in response variable (weight) at each level found in mom education level data.
  5. Thus, Mom education level has significant effect on infant's birthweight.
Here, we can clearly see LS mean infant birth weight is found to be higher in secondary mom education level.

  • The plot clearly shows that higher the education level of mother higher the infant birth weight, which can be due to many reasons such as awareness about having proper nutrition during pregnancy period. However, graduate mother showed lower infant birth weight. It might be due to diet habits, issues during pregnancy or negligence because of hectic work schedule in work place. As it is more likely that graduate mothers may opt for corporate jobs.
Diffogram

  • This plot shows that there is significant mean difference in infant birth weight across all levels present in our predictor (mom education level).
  • Overall, higher infant birth weight mean difference is seen in between secondary level and other levels present in predictor.

Code explanation:

  1. Interaction plots: intplot are displayed in this GLM procedure.
  2. The interaction plot will be sliced vertically by origin levels (factor levels present in origin variable).
  3. Store statement: stored the interaction model (int1) in work library.
Results:
First part

First part:

  1. The third table shows that the predictor variables have significant effect on variation found in response variable.
  2. The interaction of these two variables is also significant at 5% and 1% level of significance.
Second part
Second part:

  1. When type 3 sum of squares considered the interaction effect and individual effect of predictors on response variable was found to be significant.


  • This is the interaction plot that we called in GLM procedure, it is seen that the cars originated from Europe and USA with front drive train design has significant interaction such that it has effect on weight of cars that are manufactured.
Third part
Third part:

  1. The Tukey multiple test comparison shows that weight of car that has "ALL" drive train and "FRONT" drive train and which originated in USA and Asia, have significant mean weight difference with the cars that have "ALL" drive train design and were originated in Asia. In such way, you can identify significant mean difference in weight of cars in all the 9 by 9 combinations of both factors.
Fourth part

Fourth part:

  1.  The slice=origin option slices LS means by origin class variable denoting that there is significant mean weight difference in cars originated in Asia, Europe and USA with respective drive train design.
INT ELEMENT THAT WAS STORED: WORK.INT1

Code explanation:

  1. PLM : used for postfitting statistical analysis.
  2. Restore statement: calls INT1 object created in GLM procedure to processed in PLM procedure
  3. slice statement: slices according to interacting in two variables.
  4. Tukey test: again for multiple comparison test.
  5. Sliceby: to divide plot according to the classification variable mentioned.
  6. Effect plot: mentioning interaction plot which is again divided by origin factor and here we have asked for confidence limits in this plot.
Result:

A

A:

  • In third table, the front and rear combination where origin is Asia, there are no significant difference in mean weight of car with front and rear drive train design that are originated in Asia. at 5% of level of significance.
Diffogram for Origin=Asia and Drive train design interaction effect on weight of car

B

B:

  1. In third table, there is no significant mean weight difference of cars which have front and rear drive train design, originated in Europe at 5% level of significance.
Diffogram for Origin=Europe and Drive train design interaction effect on weight of car.

C

C:

  1. In third table, there is significant mean difference of weight of car at every level of drive train design, originated in USA at 5% level of significance.
Diffogram for Origin=USA and Drive train design interaction effect on weight of car.
CLM statistic of effect interaction plot.

  • The above plot shows how weight (lbs) of car, its confidence limits and center point as its mean across all the three drive train designs. The confidence limits within drive train designs are classified and displayed according to the origin of car.

Reference  links:

https://support.sas.com/rnd/app/stat/procedures/plm.html

https://statisticsbyjim.com/regression/interaction-effects/

https://www.researchgate.net/figure/Diffogram-for-pairwise-comparisons-of-the-means-shown-in-Figure-2B-Colored-segments_fig2_338482288


HOPE YOU FIND THIS BLOG INFORMATIVE.👍

Comments

Post a Comment